Kriptográfia alapok - Nyílvános kulcsú titkosítás

Szimmetrikus kriptográfia

A klasszikus titkosítási módszerek, amelyeket használtak egészen mostanáig arra alapoznak, hogy a titkosításhoz (encryption) és a feloldáshoz (decryption) is ugyanaz a kulcs használatos. Ez azt igényli, hogy a kulcsot valami titkos közegben kellene átadnunk a második félnek anélkül, hogy egy harmadik fél ne szerezzen róla tudomást, hiszen akkor az összes titkosított üzenetünket olvasni tudná. Ez kicsit ilyen “tyúk vagy a tojás” probléma, hiszen pont arra akarnánk használni a kulcsot, hogy megteremtsük ezt a titkosított közeget. Illetve ekkor, teljesen meg kell bíznunk a második félben, hiszen miután megosztottuk vele a kulcsunkat, az teljesen az ő döntése lesz, hogy azt nem e adja tovább másnak.

Tegyük fel, hogy a bankba besétálunk és a fiókunkhoz elkéri a recepciós a jelszót. Ha egy kicsit is korrumpálható a recepciós, akkor a fiókunk jelszava könnyen nem kívánatos emberek kezébe kerülhet. Ehhez a problémához még visszatérek, addig is gondolkozz egy megoldáson.

Az Enigma is szimmetrikus kriptográfia szerint működött és mint titkosítás a korában egyedülálló és példátlan volt. Komoly szürkeállománynak kellett összeülnie a Szövetségesek oldalán, hogy feltörjék. - Sokan úgy tudják, többek között a Kódjátszma film miatt, hogy az angolok törték fel először, de a valóságban a lengyelek már 1932-ben tudták olvasni a titkos üzeneteket, 1939-ben adták át eredményeiket a francia és angol kódfejtőknek. Ettől függetlenül érdemes megnézni, Alan Turing és csapatának illetve automatájának (kezdetleges számítógép) jelentős szerepe volt a későbbi, fejlettebb modellek üzeneteinek feltörésében. - Szó sincs arról, hogy a titkosításban találtak hibát. Mint mindig az informatikában, a gyenge láncszem és a legnagyobb sérülékenység itt is az ember volt. A katonák nem minden nap cseréltek kódot, ahogy azt kellett volna, illetve az üzenetekben lévő ismétlődő kifejezések mint például a “WETTERVORHERSAGE” (időjárás előrejelzés) vagy az “EINS” (egy) egyszerűsítették a kódfejtő dolgát. Érdekesség, hogy 1982-ben is használták még az Enigmát még pedig az argentínok, Fakland-szigeteki háborúban. Nagyot néztek mikor az angolok minden lépésüket tudták előre. Nem lehet hibáztatni az argentínokat, hiszen az Egyesült Királyság sose hozta nyílvánosságra az eredményeiket az Enigma feltörésében, így még mindig az volt a köztudat, hogy az Enigma titkos.

Csak azért hoztam föl az Enigmát, mert egy jó példa arra, hogy a szimmetrikus titkosítás önmagában miért nem elég. Gondolkoztál már azon, hogy az Enigmát miért csak tengeralatjárókon használták? Azért mert a tengeralatjáró ha megsemmisül, akkor az Enigmát is viszi magával a tengerfenékre, így nem lehet a gépet, azaz a titkosítást visszafejteni illetve a kódot ellopni. Ezért nem használták szárazföldi csapatoknál. Tehát nem volt skálázható, hiszen több ember esetén egyre nagyobb lett volna az esélye a kód kitudódásának. Az internet térnyerésével, és a felhasználók exponenciális növekedésével pedig a szükség egy skálázható titkosítási szabványra nőttön-nőtt.

Aszimmetrikus kriptográfia

Az aszimmetrikus kriptográfiában, avagy nyílvános kulcsú titkosításnál kulcs párokról beszélünk, ahol van egy privát kulcs és egy publikus kulcs. Retrospektíven, úgy a székben hátradőlve nézve a koncepció egyszerűsítve az alábbi: páronként a titkosításhoz szükséges kulcs publikus, a feloldáshoz a kulcs pedig titkos, és a publikus kulcsból visszafejteni a titkos kulcsot algoritmusokkal annyi időbe telne, hogy nem csak a kávénk hűlne ki, de még a Naprendszer is. Az aszimmetrikus jelző innen jön, hogy a titkosítás és dekódolás nem ugyanúgy megy.

Egy információ csere aszimmetrikus titkosítást használva Bob és Alice között az alábbiak szerint zajlana le az ábrát követve:

1. Bob letitkosítja az üzenetét Alice publikus kulcsával, majd elküldi Alicenak az eredményt.
2. Alice megkapja a titkosított üzenetet, majd a titkos kulcsával feloldja azt.

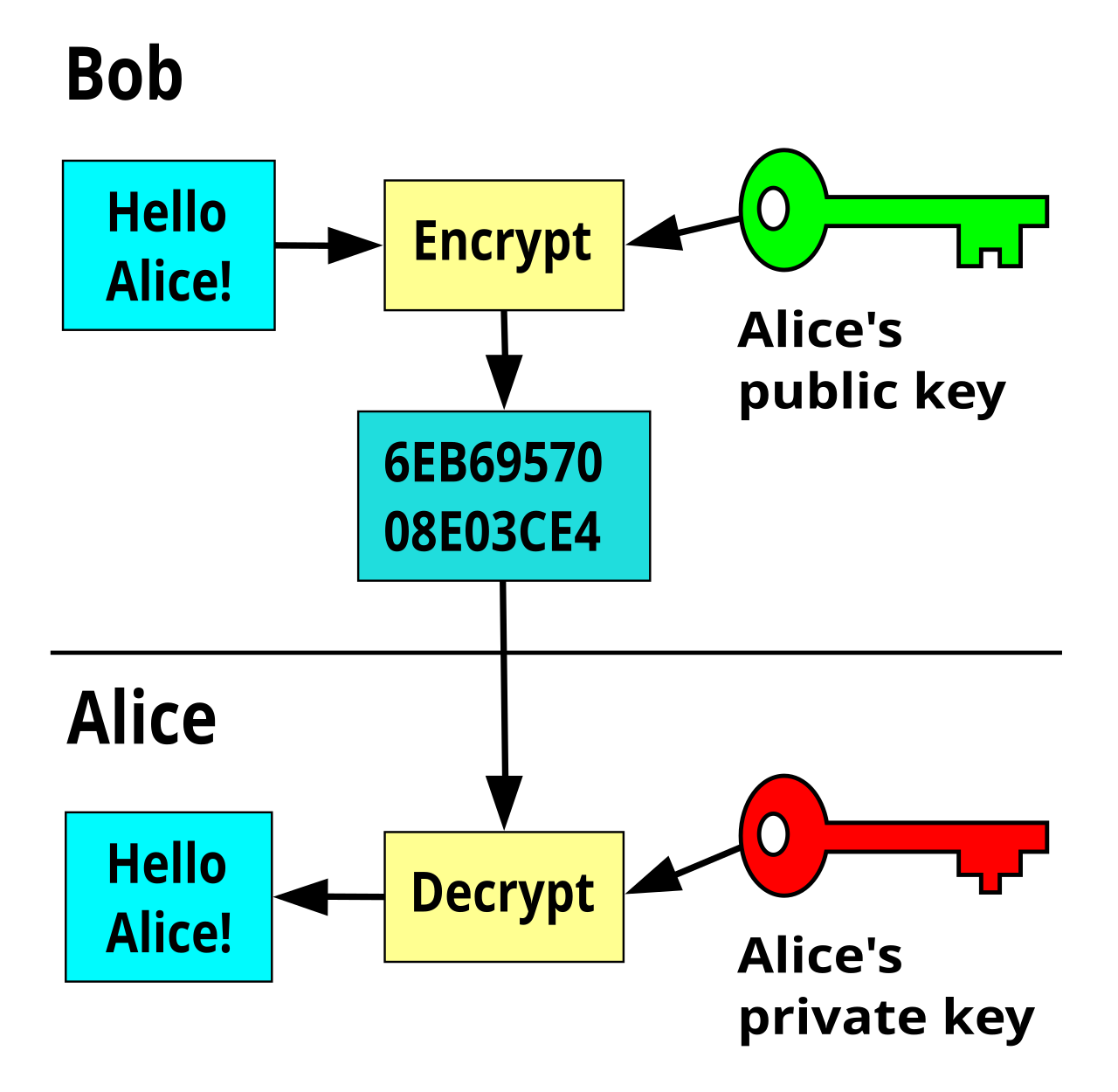
Az egész rendszer müködése azon alapszik, hogy a titkos kulcsok titkosak maradnak és senkivel nem osztjuk meg azt, mivel annak beláthatatlan következményei lehetnek ránk nézve.

Most pedig konkrét megvalósítások.

RSA (Rivest–Shamir–Adleman)

Az RSA az egy kriptográfiában nevezetes algortimus amely nyílvános kulcsú titkosítást valósít meg, melyet 1977-ben vázolt a nevében is szereplő 3 dzsentlmen.

Definíciók

Az alap ötlet az RSA mögött, hogy adott \(n, e\) és \(d\) egész számnál, az \(x \in N: 0 \leq x < n\) szám esetén az \((x^e)^d\) és \(x\) azonos maradékot adnak \(n\)-nel osztva, azaz kongruensek moduló n:

\[(x^e)^d \equiv x \pmod n\]

Ugyanakkor ha csak az \(n\) és \(e\) szám adott, a \(d\) szám kiszámítása borzasztóan nehéz. Most nem úgy értem a nehezet, mint hogy nehéz reggel kikelni az ágyból, hanem úgy hogy ha világ összes számítógépe is rendelkezésünkre állna akkor is még a temetésünkön számolnának.

Az \(n\) és \(e\) természetes számok alkotják a publikus kulcsot, melyben az \(n\) a moduló amely \(p\) és \(q\) prímszám szorzatából áll, és az \(e\) pedig a titkosításhoz használt (“e” for encryption) hatványkitevő mely relatív prím \(\phi(n)\) számmal.

a \(\phi(n)\) függvény az az Euler-féle phí függvény mely megadja, hogy \(x \in N: 1 \leq x \leq n\) számok között mennyi n-hez relatív prím van.

A \(p\) és \(q\) alkotják a titkos kulcsot, melyekbők kiszámítható a \(d\) (“d” for decryption) hatványkitevő, ami a dekódoláshoz fog kelleni. Igazából a \(p\) és \(q\) eldobható miután \(d\) ki lett számítva.

A titkosítás folyamata:

Kulcs generálás

1. Generáljunk 2 nagy \(p\) és \(q\) prímszámot. A lényeg az lesz, hogy az \(n\) számból minél nehezebb legyen prím faktorizációval megkapni a \(p\) és \(q\) számot. Ehhez a \(p\) és \(q\) is legyen lehetőleg teljesen véletlenszerű, kellően nagy és kettőjük különbsége is legyen nagy. Hatékony prím generálásra a prím tesztelése véletlenszámokra. Fontos hogy a véletlenszám generátorunk legyen minél “véletlenebb”, azaz entrópiája minél nagyobb, hiszen számítógépen csak pszeudo véletlent ismerünk hiszen a számítógép önmagában determinisztikus. Ezzel egy külön ágazat foglalkozik a matematikában, csak érdekességnek hoztam föl.

2. Számoljuk ki \(n=p * q\). Biztonságosnak ítélt kulcs azaz \(n\) hossz az 2048 bit, ami kb 617 számjegynek felel meg a tízes számrendszerben azaz értéke saccperkb \(10^{616}\). Most álljunk meg és gondolkozzunk el ezen nagyságon egy picit. Ugyebár úgy tudnánk támadóként feltörni a titkosítást, ha \(n\)-ből meg tudnánk kapni \(p\)-t és \(q\)-t. Ez kicsit túl lő az üzenet feltörésén, hiszen ezután az összes üzenetet fel tudnánk törni. Ez a prím faktorizáció problémája melyre mai napig nem ismert polinomiális komplexitású algoritmus, ugyanakkor nincsen az se bizonyítva, hogy nem létezik ilyen, bár ez a sejtés. Ha esetleg találnál ilyet, akkor könnyűszerrel világuralomra törhetsz, hiszen a banki tranzakciók, kriptovaluták, államtitkok és nem utolsósoron a digitális aláírások titkosítása is ezt használja. Például a szofterfrissítések is digitális aláírással ellenőrzik, hogy a hivatalos szerverről jött a frissités, de ha feltörnéd ezt, bárkinek kiadhatnád magad, ezáltal például az összes Windows gép felett átvehetnéd az irányítást egyetlen Windows frissítéssel. Érdekes, hogy az egész világrendünk, a civilizációnk egy matematikai sejtésre van bízva. Csak hogy elképzelhesd mennyi időbe is telne ha naívan elkezdenénk próbálgatni brute-force módszerrel a prímeket 2-től kezdve \(\sqrt n\)-ig: kb. \(10^{80}\) proton van a megfigyelhető világegyetemen, tegyük fel hogy ez mind egy olyan számításiegység ami 4 GHz-en müködik azaz az egyszerűség kedvéért másodpercenként \(4 * 10^9\) prím tesztelésére képes, tehát másodpercenként \(4 * 10^{89}\) szám tesztelésére vagyunk képesek összesen. Ezek szerint \(\frac{\sqrt{10^{616}}}{4 * 10^{89}} \approx 10^{218} \) másodpercre lenne szükségünk. Az univerzum 13,7 milliárd éves azaz kb \(4,3 * 10^{17}\) másodperc éves. Remélem ez a kis gondolatkísérlet kontextusba helyezte a nagyságokat.

3. Válasszunk ki egy természetes számot az \(e\) számára úgy, hogy \((e,\phi(n))=1\), azaz relatív prímek. Itt a hossz nem annyira lényeges mint az \(n\) esetén, tipikus érték az \(e\)-nek a \(65537\).

4. Számoljuk ki a \(d\) értékét a \(p\) és \(q\) számok segítségével. Hogy hogyan azt a helyesség bizonyításánál méltatom bemutatni.

Tehát ezek után van egy publikus kódoló függvényünk

\[C: x \mapsto x^e \pmod n\]

ahol \(x:=\) a plaintext üzenetünk azaz a titkosítandó adat

és van egy titkos dekódoló függvényünk

\[D: y \mapsto y^d \pmod n\]

ahol teljesül az hogy \(D(C(x))=x\)

Aki eddig eljutott és ismeri a hatványazonosságokat az biztos elgondolkozott rajta, hogy a \(d\) és \(e\) felcserélhető-e. Bizony felcserélhetőek hiszen \((x^e)^d = (x^d)^e\). Azt nem mondanám, hogy használható lenne a titkos kulcs titkosításra, mivel nem lesz tőle titkos, hiszen bárki feloldhatja a hozzátartozó publikus kulccsal. Ezt a kommutatívitást is ki tudjuk használni a gyakorlatban a digitális aláírásnál és azonosításnál, de erről többet kicsit lejebb :).

Kulcs megosztása

Bob és Alice az RSA-t akarják használni tikosításra beszélgetés közben, mert biztonságos. Ekkor ha Bob üzenetet szeretne küldeni Alicenak, akkor elkéri Alice publikus kulcsát \((n,e)\), majd ezt egy csatornán (nem muszáj biztonságosnak lennie) meg is kapja. Alice a titkos kulcsát \((d)\) soha nem adja ki, azt a dekódolásra használja saját magánál.

Titkosítás

Bob miután megkapta Alice publikus kulcsát, azt felhasználva titkosítja az \(x\) üzenetet és megkapja titkosított szöveget \(c\)-t.

\[c \equiv x^e \pmod n\]

Minden józan, már tapasztaltabb emberben, fel kell merülnie annak az ördögi kérdésnek, hogy ez a lépés vajon polinomiális-e mert ha nem akkor semmi értelme nincsen az egésznek. Szerencsére a moduláris hatványozás megoldható polinomiálisan az ismételt négyzetre emelés módszerével, annak ellenére, hogy a hatványozás önmagában nem lenne polinomiálisan kivitelezhető.

Feloldás

Alice ezután megkapja a titkosított üzenetet és a titkos kulcs segítségével feloldja azt.

\[c^d \equiv (x^e)^d \equiv x \pmod n\]

Helyesség bizonyítása

Eddig valjuk be őszintén a levegőbe beszéltem, semmi se lett bizonytva, már pedig ez így nem járja.

Cél hogy bebizonyítsuk, hogy \[\forall n \in N, n=p * q, \forall e \in N, (e,\phi(n))=1\] esetén \(\exists d\) ahol igaz az, hogy \((x^e)^d \equiv x \pmod n\) ahol \(x\) tetszőleges üzenet.

Ehhez felhasználjuk az Euler-Fermat tételt miszerint

ha \(n \leq 1\) és \((x,n)=1\) \(\Rightarrow x^{\phi(n)} \equiv 1 \pmod n\)

Emeljük a konkruenciát \(k \in N\)-ra és szorozzuk mindkét oldalát \(x\)-szel. Ezek ekvivalens lépések, ekkor

\[x^{k\phi(n) + 1} \equiv x \pmod n\]

tehát ha a hatványkitevő \(ed = k\phi(n) + 1\) akkor igaz a kongruencia.

Ebből a megállapításból az alábbi kongruencia következik

\[ed \equiv 1 \pmod {\phi(n)}\]

hiszen ez az előbbi állítással ekvivalens.

Ez pedig egy lineáris kongruencia a \(d\) ismeretlenre, hiszen \(e\) értéke adott és \(\phi(n) = (p-1)(q-1)\) itt nem tárgyalt azonosságok alapján. Ennek a lin. kon. biztosan \(\exists\) megoldása, mivel \((e,\phi(n))=1\). Ezt a megoldást hatékonyan meg is tudjuk találni az Euklideszi algortimussal.

Ez nem a teljes bizonyítás hiszen nem fedtük le azt az esetet amikor is \((x,n) \neq 1\). Ennek a gyakorlati valószínüsége ámbár nagyon kevés hiszen ez azt jelenti, hogy \(p | x\) vagy \(q | x\), de mégis kell vele foglalkozni, hiszen matematikusok vagyunk :D.

Ha \(p | x\) és \(q | x\) is akkor \(pq | x\) azaz \(n | x\) ekkor \(x^{k\phi(n) + 1} \equiv x \pmod n\) természetes hogy létezik megoldás hiszen \(x \equiv 0 \pmod n\) és \(x^{k\phi(n) + 1} \equiv 0 \pmod n\) hiszen ha \(n | x\) akkor \(x\) többszörösei is oszthatóak \(n\)-nel.

Ha \(p | x\) és \( q \nmid x\) akkor külön-külön bemutatjuk

1. \[x^{k\phi(n) + 1} \equiv x \pmod q\]

2. \[x^{k\phi(n) + 1} \equiv x \pmod p\]

kongruenciát is, hiszen ekvivalens ez \(x^{k\phi(n) + 1} \equiv x \pmod n\)-nel

Az 1. állítás bizonyítása 1:1 megegyezik azzal az esettel mikor \((n,x)=1\) hiszen most \((q,x)=1\). A 2. állítás pedig szinte ugyanaz mint amikor \(x \equiv 0 \pmod n\).

Ha \(p \nmid x\) és \( q | x\) akkor az előző esethez szimmetrikusan, hasonlóan bizonyíthatunk csak \(q\) és \(p\) szerepét felcserélve.

Most már teljes a bizonyítás!

Megjegyzések a gyakorlati alkalmazáshoz

A dekódolás folyamatában, az 1 nagy hatványkitevős ismételt négyzetre emelést érdemes lecserélni 2 kisebb kitevős ismételt négyzetre emelésre, és ez ekvivalens is lesz a kínai maradéktétel miatt, ugyanakkor kisebb hatványkitevővel dolgozik ez a 2 ismételt négyzetre emelés ami a gyakorlatban gyorsabb mint az 1 nagy hatványkitevővel. A részletekbe most nem megyek bele.

Most pedig térjünk rá a biztonságra, ami egy titkosításnál sarkalatos pont úgy hiszem. Már eset róla szó hogy az egész RSA biztonsága az a faktorizációs problémára épül. Ahogy már említettem kulcs hossznál már a 2048 bit ajánlott, bár még nem ismert olyan eset, hogy 1024 bites kulcsot praktikus időn belül feltörtek volna. 512 bites kulcsokat még nem de már ennél rövidebb kulcsokat talán már 20 évvel ezelőtt is feltörtek gépparkokkal, ma már egy asztali számítógép is megtudja csinálni reális időn belül. Az aktuális viszont a kérdés, hogy a kvantumszámítógépek megjelenése mennyire zavarja meg ezt a magabiztosságot. Rosszul fogalmaztam mert ez már 1994 óta nem is kérdés, mivel Peter Shor bemutatta, hogy ha valaha keletkezik kvantumszámítógép, akkor azon polinomiális időn belül törhető lesz az RSA. Emiatt nemzet szintű szervezetek és játékosok, illetve most már applikációk is (pl. Signal, Messenger) kezdenek átállni kvantum rezisztens titkosításokra.

Nem feltétlenül kell viszont hatalmas magaslatokban gondolkodni ha RSA sérülékenységről van szó. Elég csak egy rossz konfiguráció. Például ha \(e=3\) azaz túl kicsi, akkor könnyen meglehet hogy \(x^e < n\) és ilyenkor csak elég \(e\)-dik gyökét venni a titkosított üzenetnek, és mivel nem jászott a modulus, ezért megkapjuk gond nélkül az üzenetet. Ez amatőr dolog, gyakorlatban nem megszokott de például CTF feladatban előfordulhat. Kulcs generálásnál is már említettem, hogy rendkívül fontos az eléggé random véletlenszám generátor, ami nem kis feladat. Hallottam, hogy például valamilyen nagy cég lávalámpa mátrixot használt, ahol a lávalámpákban mozgó kis buborékok mozgását figyelték és ezek alapján generáltak véletlenszámot.

A csupasz RSA determinisztikus, tehát ugyanaz a kulcs ugyanazt az üzenetet, ugyanazt a titkosított szöveget köpi ki. Ebből az következik, hogy a támadóknak lehetősgük van idő-tárhely “trade-off”-ra. Ez hasonlít a hash függvények elleni támadásra, ahol úgynevezett “rainbow table”-lel előre lehashelnek rengeteg előfordulható szöveget (főképp jelszavakat) majd eltárolják az eredményeket. Itt is ez a helyzet, a nyílvános publikus kulccsal letitkosítunk temérdek variációt és eltároljuk őket, majd ha valamit vissza akarunk fejteni, csak megkeressük a hatalmas adatbázisunkban, hogy van-e egyezés. Félelemre semmi ok, pontosan ugyanúgy lehet védekezni ez ellen is mint a rainbow table-ök ellen is. Ott a salting azaz sózásnak hívták, itt padding-nek nevezik. Padding-nél az üzenetet bizonyos protokoll szerint kiegészítjük egy véletlenszerű toldással, majd ezt feloldásnál visszafele eljátszuk.

Ami engem izgat és biztosan meg fogom csinálni a gyakorlatban, azok a side-channel támadások. Ezek arra alapoznak, hogy a támadónak hozzáférése van plusz információkhoz a titkosítás során, például hogy milyen hardveren történik, mennyi idő alatt, mekkora teljesítményt igényel, mennyi hőt vagy elektromágneses hullámokat bocsájt ki a processzor a titkosítás alatt. Olyan titkosítás nem létezik amely side-channel támadással ne lehetne feltörni, mivel az implementációt nem lehet tökéletesre megcsinálni. Viszont ehhez fizikai hozzáférésre lenne szükségünk a számítógéphez amely szerencsére nagyban csökkenti a támadók esélyeit.

Diffie-Hellman

Az RSA képes hatalmas üzenetek blokkonkénti titkosítására a tárgyalt aszimmetrikus algoritmussal, de az igazság az, hogy bármennyire is próbálkozunk optimalizálni, egy szimmetrikus titkosítás mindig gyorsabb lesz nála. A szimmetikus titkosításnak viszont szüksége van egy közös titkos kulcsra amely titkosan lett megosztva a felek közöt, ezt a problémát már a cikk elegén túltárgyaltam. Tehát az aszimmetrikus és szimmetrikus titkosításnak is megvannak előnyei és hátrányai. Mit csináltak a zseniális mérnökök? Mindkettőt használják egyszerre megtartva a jó tulajdonságokat a rosszaktól pedig megszabadulva. Ezért az internet vadvilágában az a szabvány, hogy A és B eszköz aszimmetrikus titkosítással közös titkos kulcson megegyeznek, majd ezután egy megegyezett szimmetrikus titkosításra átváltanak. Lenyűgöző, nem?

Itt jön képbe a Diffie-Hellman-kulcscsere, ami időben meg is előzte az RSA-t, az 1976-os megjelenésével. Az elismerés érte Ralph Merkle-t, Whitfield Diffie-t és Martin Hellmant-t érdemli. Az algoritmus célja, hogy nyílvános kulcsú rejtjelezéssel, felek között megteremtsen egy közös titkot, amelyhez harmdik fél hozzáférni nem tudhatott. Ezt az RSA-hoz hasonlóan egy olyan függvénnyel teszi ami egyirányú.

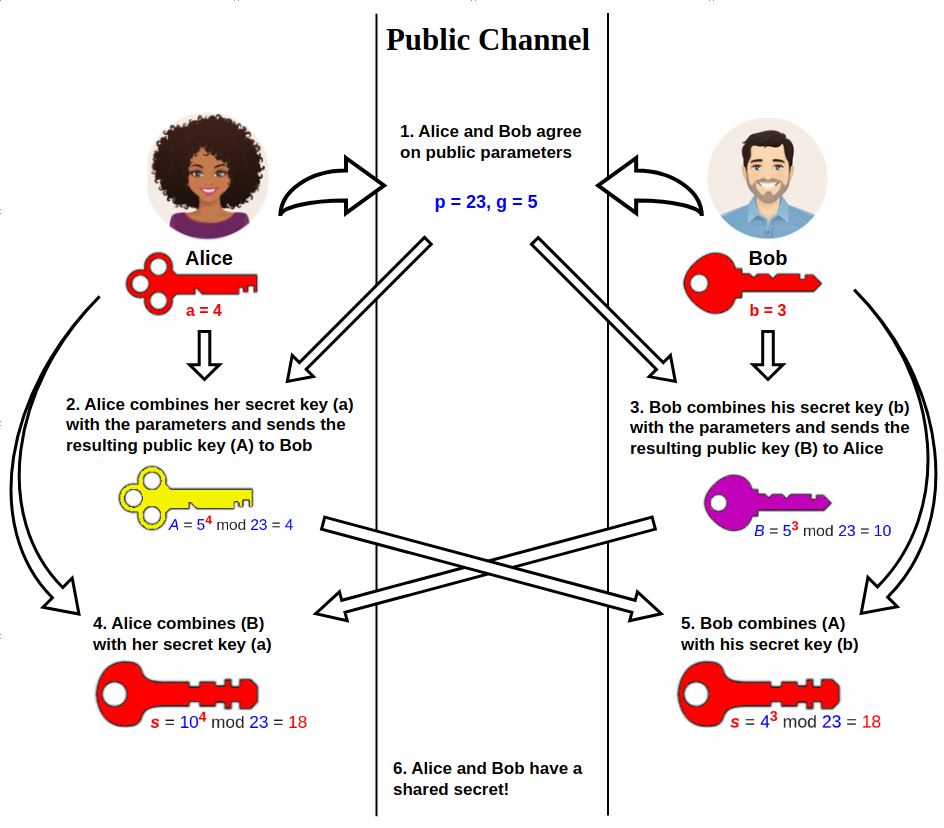
Wikipédián találtam ezt a remek kis egyszerű ábrát amit követve könnyen meg lehet érteni a fő gondolatot.

A folyamat az alábbi:

Alice és Bob megegyeznek publikusan \(p,g \in N\) számokról (ábrával ellentétben, nagyságrendben nagyobb számokat használva).

Alice és Bob is külön-külön felhasználják titkos kulcsaikat. Alicenál, az \(a, \in N\) titkos kulccsal:

\[A=g^a \pmod p\]

Bobnál, a \(b, \in N\) titkos kulccsal:

\[B=g^b \pmod p\]

Majd \(A\)-t Alice elküldi publikusan Bobnak, Bob pedig \(B\)-t Alicenak.

Ezután mindkettőjük a kapott értéken megint felhasználják titkos kulcsukat. A keletkező \(s\) szám lesz a közös titok.

Az algoritmus fő ötlete, hogy kihasználja az alábbi összefüggést

\[g^{ab} \equiv g^{ba} \pmod p\]

Ez teszi lehetővé, hogy Alice és Bob is ugyanazt az értéket kapja meg. Mi állítja meg a támadókat a privát kulcsok visszafejtésére vagy akár a közös titok kiderítésétől?

Itt is egy olyan matematikai függvényen alapszik a biztonság, amelyről azt sejtjük, hogy nem lehet polinomiális időn belül (a kvantumszámítógépeket nem beleértve ebbe megint) elvégezni. Ez a függvény a diszkrét logaritmus. Egyszerűen arról van szó, hogy \(g^a,g^b,p,g\) ismeretével nem tudjuk visszafejteni \(a,b,g^{ab}\) értékeket még mielőtt a Nap kihűlne.

Gyakorlat

A fentiekben is már bőven szó esett arról, hogy mire is lehet használni az aszimmetrikus kriptográfiát, de talán most jobban kifejtem.

TLS

A TLS (Transport Layer Security), egy olyan keretrendszer, szabvány, amely azon protokollok biztonságáért felelős mint például a HTTPS, amelyek A címtől juttatnak el B címre adatokat. Tehát lényegében azt testesíti meg, ami eddig a cél volt, hogy az internet kommunikáció titkosítva legyen. A TLS jóformán az amit, a Diffie-Hellman-kulcscserénél már elmondtam, hogy asszimetikus titkosítással megegyezünk egy közös titkos majd átállunk szimmetikusra ezzel a titokkal, mivel az gyorsabb. Azonban az olyan részleteket kihagytam, mint például hogy azon is ilyenkor egyeznek meg milyen titkosítást használjanak, amelyre mindkettő eszköz képes.

Fontos feladata a TLS-nek az autentikáció is. Például hiába a sok erőfeszítés ha kivetelezhető egy MITM (Man-In-The-Middle) támadás. Az MITM során a támadó harmadik félként beáll Alice és Bob kommunikációja közé, úgy hogy ezt sem Alice nem veszi észre sem Bob. Ez úgy lehetséges, hogy a támadó, mondjuk József, azt állítja Alicenak, hogy ő Bob, Bobnak pedig azt mondja hogy ő Alice. Így Alice és Bob is József publikus kulcsával fogja titkosítani a kommunikációját, ezért József bármikor beleolvashat abba. Fontos, hogy ahhoz hogy az illúzió működjön, József a kommunikációt továbbítja Alice és Bob között, így a két szereplőnek tényleg fogalma sem lehet hogy valójában valakin keresztül megy az üzenetük.

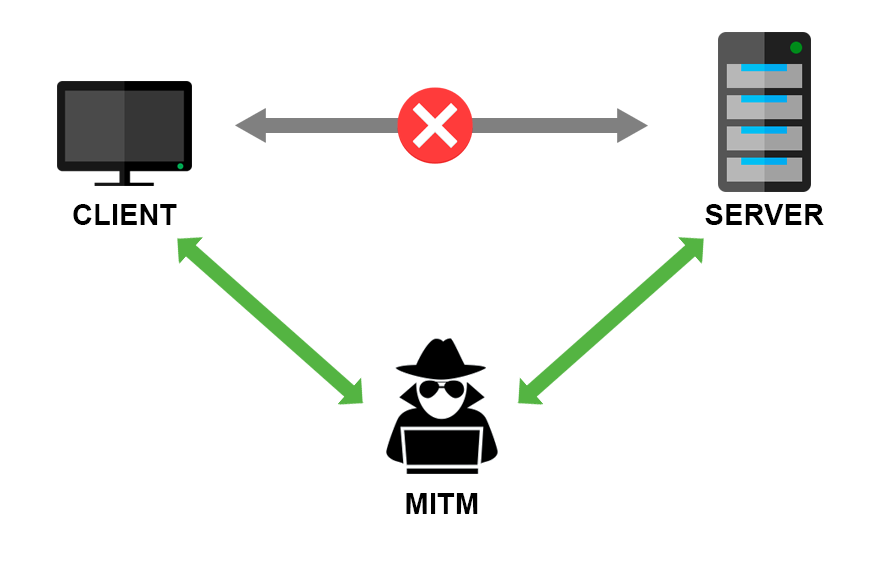
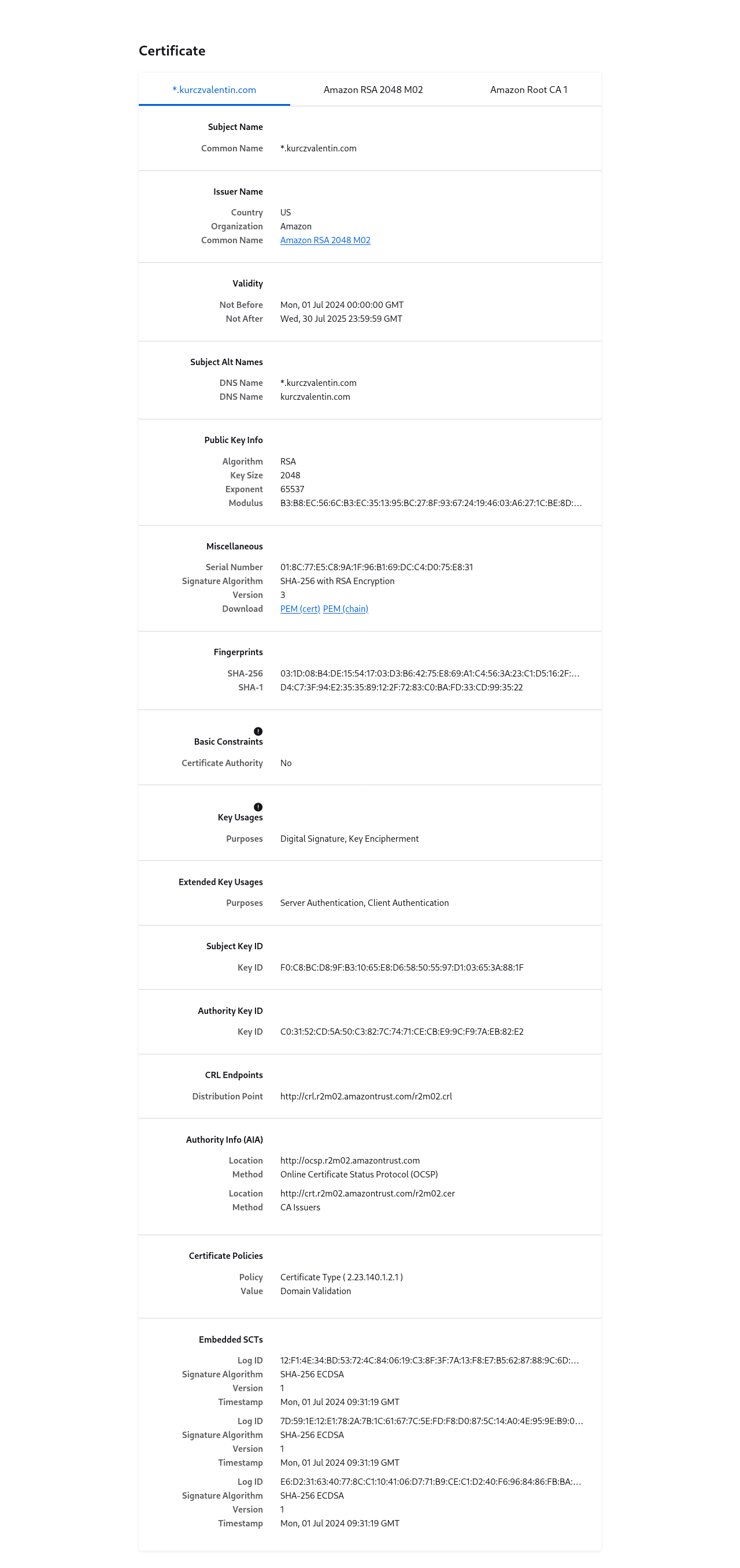
Erre a megoldások voltak a tanusítványok. Tanusítványokat megbízott harmadik felek állítják elő, és egy tanusítványban szerepel, hogy az adott félhez milyen publikus kulcs tartozik. Ezek az SSL tanusítványok, melyeket te is részletesen el tudsz olvasni bármelyik weboldalnál ha a böngésződben a lakatra kattintasz. Itt van például az enyém:

Challange-response

Minden eszköz most már rendelkezésünkre áll ahhoz, hogy megoldjuk a korrupt recepciós problémát. A cél az, hogy a recepcióssal ne kelljen megosztanunk semmi titkosat, de ugyanakkor a recepciós 100%-ban biztos lehessen, hogy azok vagyunk akiknek állítjuk magunkat. Mi sem egyszerűbb: a recepciós a tanusítvány szerint Kurz Valentinhez tartozó publikus kulccsal letitkosít valami számára egyedi dolgot, mondjuk egy véletlenszámot, és elküldi azt nekem - ez a challange. Majd én ezt feloldom a titkos kulcsommal, és visszaküldöm neki az eredményt - ez a response. A jó eredményt valóban csak is én tudom megmondani (már ha tényleg én vagyok Kurcz Valentin :D), hiszen csak az én titkos kulcsommal lehet feloldani a hozzám tartozó publikus kulccsal titkosított üzeneteket. A korrupt recepciós pedig a kardjába dőlhet mert nem sikerült kicsalnia belőlünk a titkunkat.

Ezt a challange-response rendszert használja a legtöbb SSH kliens is, amikor távolról szeretnénk elérni egy shell-t. A szerver autentikálja a klienst, hogy meggyőződjön jogosultságairól.

Digitális aláírás

Autentikációra van más módszer és erre példa a digitális aláírás. Hasznossága kétségbevonhatatlan, hazánkban is már az Ügyfélkapun keresztül alá tudunk írni hivatalos okmányokat, és nemhogy legalább annyira hiteles mint a tinta és papír, de megfelelő konfiguráció mellett, meghamisíthatlan nem úgy mint az írásunk.

Az RSA című elbeszélő költeményemben már szó esett arról, hogy a titkos és a publikus kulcs funkcionalitása felcserélhető (kommmutatívak), nem úgy mint például a Diffie-Hellman esetében. Ezt a tulajdonságot kombinálva egy biztonságos hash függvénnyel és megkapjuk a gyakorlatilag meghamisíthatlan aláírást, ami az aláírt üzenetek integritását is ellenőrzi. A folyamat a következő:

1. Az aláírandó dokumentumot leképezzük egy hash értékre.

2. Ezt a hash értéket kombináljuk az RSA algoritmusával a titkos kulccsal (direkt nem titkosítást mondtam)

3. Majd ennek a végeredményét mellékeljük mint aláírás a dokumentumunk mellé.

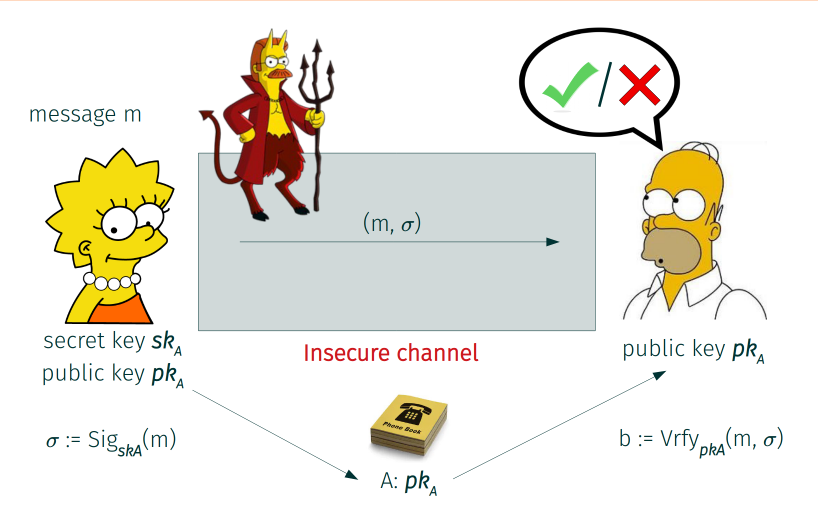
Aki ellenőrizni szeretné az aláírást, csak annyi a dolga, hogy a dokumentumot hasheli, és az aláírást kombinálja a feltételezett aláíró publikus kulcsával, és ha az eredmény egyezik az előbbi hashel, akkor biztosak lehetünk, hogy ő írta alá.

A hashelés lépése több szempontból is kézenfekvő:

• Mivel bármilyen nagy dokumentumra, ugyanolyan hosszú hash digest-et képez (pl SHA256 esetén 32 byte hosszúságút) ezért a titkos kulccsal való kombinálás gyorsabban megy.

• Hashelés egyik természetes haszna az integritás ellenőrzése, hiszen a legisebb változás is a bemenetben, teljesen más hash digest-et eredményezhet. Így ha a dokumentum, amit aláírtunk az ellenőrzés előtt az úton valahol manipulálva, módosítva lett, akkor az aláírás érvénytelenődik.

Fontos megjegyzés az is, hogy ha egyszer valami aláírva lett, utána letagadni azt nem lehet, hiszen senki más nem írhatta alá.

Ennek a biztonsága is azon múlik, hogy semmilyen titkos kulcs nem kerül illetéktelen kezekbe, mert ha ez megtörténik, utána a támadó az ellopott kulcs tulajdonosának adhatja ki magát bárhol, bármikor. Ennek a következmé Sajnos ilyenek történnek, ezért kell valami immunitás ez ellen. Ezért vezették be a kulcsok érvénytelenítését, amiket akkor használunk ha kulcsunkat ellopták és nem akarjuk, hogy felhasználhassák őket.

Összegzés

Sikerült összefoglalni felső nézetből az asszimetikus rejtjelezést, néhol belemenni a részletekbe is, példákkal ellátva. Jelenleg is kezdő pályán vagyok ebben a témában szóval könnyen előfordul, hogy valahol nem pontosan fogalmaztam. Ebben az esetben szólj és kijavítom.

Irodalom amit használtam/olvastam: Applied Cryptography, Second Edition: Protocols, Algorthms, and Source Code in C

Források

https://people.csail.mit.edu/alinush/6.858-fall-2014/l16-timing-attacks.html

https://en.wikipedia.org/wiki/RSA_(cryptosystem)