Lokalitástudatos programozás
Neumann architektúrája óta, egy számítógép müködése során, a futtatandó utasításokat, és ezen utasítások által hivatkozott címek tartalmát is egy memóriában tárolja. A programban használt adatok, úgynevezett adatmemóriból érhetőek el, ez pedig tárhierarchiába rendeződik.
Tárhierarchia
A számítógépünk teljesítménye lényegében a processzor és a memória órajeléből tevődik össze, és eme két egység közül, a memória az ami a processzor mögött kullog. Ez azt jelenti, hogy hiába a magas CPU órajel, ha a memória szűk keresztmetszetként viselkedik mellette, mivel ha az éppen végrehajtandó utasításnál, nincsen kéznél a használandó adat, akkor a processzor várakozásra kényszerül, ezáltal nem használja ki teljes potenciálját, így suboptimális lesz a kihasználtsága.
Lokalitási elvek
Nagy szerencse hogy a számítógépes programok többsége valamilyen mintát követnek, mikor a memóriába nyúlnak, úgynevezett lokalitási elveket, és ezeket kihasználva tudunk a teljesítményen javítani. Többféle lokalitási elvet is ismerünk:
Ha egy memóriában tárolt adaton műveletet végeztünk…
- Időbeli lokalitás: …akkor valószínűleg a közel jövőben is használni fogjuk. Példa: egy ciklus számlálóját minden ciklusban növelem.
- Térbeli lokalitás: …akkor valószínűleg a közelben lévő adatokat is használni fogjuk. Példa: egy tömböt bejárok.
- Algoritmikus lokalitás: Sok program dinamikus adatstruktúrákkal dolgozik (pl. bináris fák, láncolt listák), ezek viszont nem felelnek meg se nem a térbeli se nem az időbeli lokalitásnak (mivel a memóriában nem folytonosan helyezkednek el), ámde mégis szabályos viselkedést eredményeznek, melyet ki lehet használni.
Tehát ha lokalitási elvek szerint, a processzor közelébe helyezzük a gyakran használt adatokat és környezetüket, akkor csökkenthetjük a lassú és költséges memória műveletek számát. Ekkor is memóriában helyezzük el az adatainkat, csak egy sokkal gyorsabb de kisebb és magasabb fogyasztásúban. Ezt a memóriát cache memóriának nevezzük. De milyen technológiát használnak cachenél?
Több memória technológiát is ismerünk, mint például a magas adatsűrűségű és olcsóbb, de lasúbb DRAM, vagy az alacsony adatsűrűségű és drága, de gyors SRAM. Egy bit tárolásához, A DRAM 1 tranzisztort, az SRAM pedig 6-ot használ, innen ered a fogyasztás, adatsűrűség és az ár különbség. Egyiknél sem teljesülhet viszont egyszerre az, hogy olcsó, gyors és nagy, így mindig az igényekhez igazítva, a kompromisszum kötés elkerülhetetlen. Itt jön be a tárhierarchia miszerint több szintből építjük fel a memóriát úgy, hogy az adott szintet minél többször használja a processzor, annál gyorsabb és ezáltal kisebb legyen.
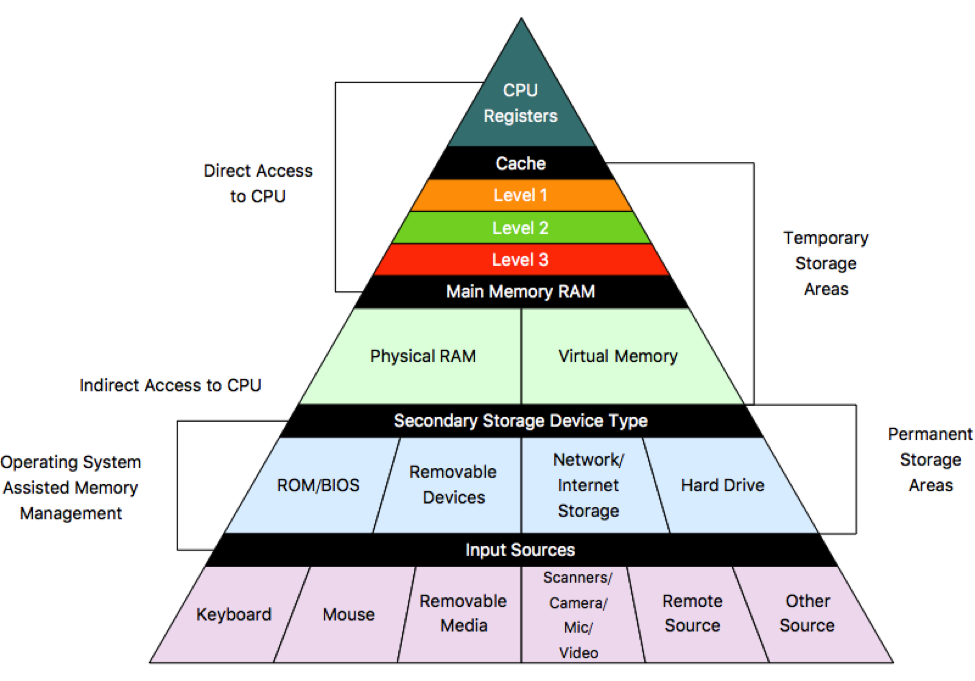
A leglassabb tárolón, a háttértáron tartjuk a legkevésbé használt, de nagy mennyiségű adatokat, általában HDD-n vagy SSD-n. A gyakran használt adatokat az operatív memóriában tároljuk, általában DRAM-ot használva, és az éppen futó program vagy process által használt adatokat (pl. egy lokális változót) pedig a cache-ben tartjuk, ami SRAM-ból épül fel.
A cache további működését itt nem részletezem, de ha érdekel akkor érdemes utánanézni, hogy mi alapján kerülnek be a cache-be az adatok, mert nyílván mikor a program hivatkozik a memóriára akkor már készen kell állnia a cache-ben, így valahogy meg kellene jósolni, hogy a jövőben használni fogjuk-e az adatot, ugyanakkor nem szemetelhetjük tele a cache-t mindennel mert kicsi :(, ezért jó tippnek kell lennie. Prefetch-nek nevezik ezt, és egyszerűbb mind aminek gondolnád.
Mind ezek szerint elengedhetetlen, hogy a processzor kihasználás érdekében, a programozó segítse a tárhierarchia munkáját:
- A cache esetében, ha a programozó össze-vissza hivatkozik a memóriára, akkor sok lesz a cache hiba, és így kénytelen lesz a számítógép a lomha memóriához nyúlni.
- A DRAM alapú rendszermemória esetében az azonos sorban lévő cellák elérése gyors, de ha itt is véletlenszerűen hivatkozunk a címekre, akkor az új sorok megnyitása költésges és lassú művelet lesz.
Tehát a programozó célja, hogy a memóriákat úgy címezze, hogy azok megfeleljenek a lokalitási elveknek. Hogyan?
Lokalitásbarát ciklusszervezés
A gyakorlatban számtalan alkalommal van szükség egy-, vagy többdimenziós tömbök bejárása, ehhez pedig ciklus(ok) szükséges(ek). Példát mutatok azon ciklusszervezési technikákra, melyek hasznosítják az imént kifejtett tárhierarchiai ismereteinket, és ezzel javítják programunk futásidejét.
Ciklusegyesítés
Eredeti kód:
for (int i=0; i < N; i++)
b[i] = c * a[i] - x;
sum = 0;
for (int i=0; i < N; i++)
sum += b[i];
for( int i=0; i < N; i++)
d[i] = a[i] + b[i];
Fenti kód egy C nyelvű mezei, iskolapélda kód. Most mindenki kapaszkodjon meg mert matekozni fogunk. Számoljuk ki a cache hiba-arányt azaz azt, hogy összes cache-hez intézett kérésünk közül mennyiszer kaptuk azt a választ, hogy sajnos a lassú memóriához kell nyúlnunk, mert a cache-ben nincsen benne az, amit keresünk. Tegyük fel az alábbiakat az egyszerűség kedvéért:
- N legyen a tömb mérete tetszőlegesen nagy
- a cache blokk mérete 64 bájt
- a tömb elemei 8 bájtos double-ök
- az i, c, x és sum elérése nem jár memória-hozzáféréssel.
Az első for ciklus bejárja az a és b tömböt. Az i = 0 -nál cache hibát kaptunk a[0] és b[0] esetben is, mivel üres volt eddig még a cache-ünk. Ha cache hiba történik akkor viszont 8 tömb elem kerül be a cachebe, mivel a térbeli lokalitás szerint azt feltételezzük, hogy a soron következő elemeket is használni fogjuk, és több már nem is férne bele egy cache blokkba (64/8=8). Tehát 8 lépésenkét lesz cache hiba, és mivel 2N memóriahivatkozás van ezért itt 2N/8 cache hiba lesz.
A második for ciklusnál, ha N elég nagy volt akkor a b tömb eleje már nincs benne a cache-ben, mert a hátsó elemei már kiszorították onnan. Ezért itt, megint minden 8. hivatkozás cache hiba lesz, így N/8 hibát okozva.
Hasonlóan számolhatunk a harmadik ciklusban is, 3N hivatkozás függvényében 3N/8 cache hibát kapunk.
Szummázva a cache hibákat megkapjuk, hogy 6N memóriahivatkozásnál 1/8 lesz a cache-hiba arány, ami 12.5%.
Most pedig ciklusegyesítéssel a kód:
sum = 0;
for (int i=0; i<N; i++){
b[i] = c * a[i] + x;
sum += b[i];
d[i] = a[i] + b[i];
}
Egyértelműen látszik, hogy ez az algoritmus ugyanazzal a funkcionalitással rendelkezik mind az eredeti, csak kicsit jobb. A ciklus hasában az első 2 memóriahivatkozás még mindig minden 8. lépésnél cache hibát okoz. A második sorban az a[i] és b[i] soha nem okozhat cache hibát, mivel már biztosan a cache-ben vannak az első sor révén. A harmadik sorban pedig az előző érvelés alapján csak a d[i] fog cache hibát dobni 8 lépésenként.
Tehát összesen 3N/8 (= 2N/8 + N/8) hibát kapunk így az arány 6N memóriahivatkozás mellett 1/16-od, ami 6.25%, azaz fele az előzőnek.
Itt látszik, hogy milyen kis energia befektetéssel, kétszer gyorsabb futásidőt kaptunk. Az első ökölszabály tehát, hogy amit lehet egyetlen ciklusban, azt egyetlen ciklusban érdemes megvalósítani.
Ciklusok sorrendjének optimalizálása
Az alábbi példában egy 2 dimenziós tömb, 2 különböző bejárásán mutatom meg, miért fontos a ciklusok sorrende.
Most először a jó példát mutatom
Bejárás sor-folytonosan:
for (int i=0; i<N; i++)
for(int j=0; j<N; j++)
sum += a[i][j];
A cache hiba vizsgálása előtt tisztázni kell, hogy C nyelv a 2 dimenziós tömböket sor-folytonosan helyezi el a memóriában. Tehát ha van egy {{4, 2}, {0, 6}} 2 dimenziós tömb akkor az a memóriában
… 4 | 2 | 0 | 6 ….. módon kap helyet
Ekkor a bejárás soronként megy végig. Ez szerencsés hiszen a térbeli lokalitás miatt sorokat fog a számítógép is a cache-be rakni. Így a feljebb kikötött feltevések és 64 bájtos blokkméret, 8 bájtos elemméret mellett az algoritmus cache hiba-aránya 1/8-ad lesz, de prefetch algoritmussal még ezen is lehetne javítani.
Most nézzük meg, hogyan NE csináljuk
Bejárás oszlop-folytonosan:
for (int j=0; j<N; j++)
for(int i=0; i<N; i++)
sum += a[i][j];
Itt felcseréltem a két ciklus sorrendjét. Ilyenkor hiába próbálja az egy sorban lévő elemeket (pl. a a[i][j+1], a[i][j+2], a[i][j+3] …) betölteni a számítógép, mert ha N > 8, akkor a[i][j] után következő a[i+1][j] nem lesz benne a cache-ben biztosan. Ha N*8 nagyobb mint a cache méret akkor még ennél is rosszabb a helyzet, mivel mire a külső ciklus lép egyet j-ből j+1-be addigra a[i][j+1] már nem lesz benne a cache-ben, hiába olvastuk be a[i][j]-nél. Tehát minden memóriahivatkozás cache hibát dob, azaz 100% az arány.
Blokkos ciklusszervezés
Van még egy további technika, az úgynevezett blokkos ciklusszervezés, amikor is blokkonként járunk be egy mátrixot. Ez például akkor tud nagy segítséget nyújtani, amikor egy mátrixot kell transzponálni:
for (int i=0; i<N; i++)
for(int j=0; j<N; j++)
b[j][i] = a[i][j];
Ekkor a-t sor-folytonosan b-t oszlop-folytonosan járjuk be, ezért a fenti példák alapján, elég nagy N esetén, b-nél 100% os lesz a cache hiba-arány. Ezen tudunk segíteni az alábbi módon:
for (bi=0; bi<=N-BLK; bi+=BLK)
for (bj=0; bj<=N-BLK; bj+=BLK)
for (i=bi; i<bi+BLK; i++)
for (j=bj; j<bj+BLK; j++)
b[j][i] = a[i][j];
Kicsit obfuszkáltnak tűnhet, de talán az ábra segít
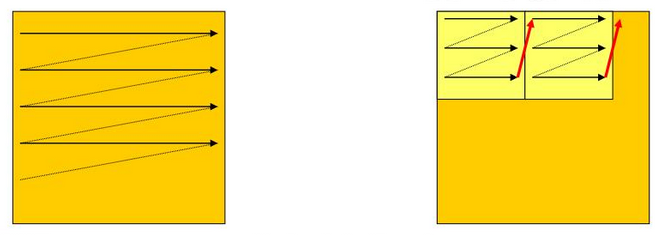
Itt csak arra kell figyelni, hogy megfelelő BLK-t, azaz blokkméretet válasszunk, mivel az egésznek az a lényege, hogy akkora blokkot válasszunk, hogy minél kevesebbszer legyen cache hiba szummázva.
Kicsit edge-case-nek tűnhet ez az egész mátrix transzponálás, de a gyakorlatban rengeteg mátrix transzponálás és mátrix művelet történik, elég csak a grafikus kártyátokra nézni, ami pontosan erre van optimalizálva, a fenti technikáknál jóval bonyolultabb módszerekkel is.
Összegzés
Tehát megismerkedtünk a számítógépünk egy fontos elemével a tárhierarchiával, azon belül is szemügyre vettük jobban a cache-t, majd pedig ezt a tudást felhasználva gyakorlati problémákra tudtunk jobb teljesítményt eredményező megoldásokat találni. Kell ennél több? :D